During my study of raytracing and browsing on Shadertoy, I have seen lots of different ways of implementing camera models for final rendering. Here is my summary for most of the solutions.

Camera Model in Raytracing in One Weekend

The previous post Raytracing - Camera and Multisampling Antialiasing documented the simplest camera setup for raytracing rendering. This camera model has fixed world position at origin, fixed image plane (or near clipping plane) size and position at (0,0,-1), pointing to the negative Z axis.

#include "ray.h"
class camera {
public:
    camera() {
        lower_left_corner = vec3(-2.0,-1.0,-1.0);
        horizontal = vec3(4.0,0.0,0.0); // horizontal range
        vertical = vec3(0.0,2.0,0.0);   // vertical range
        origin = vec3(0.0,0.0,0.0);
    }

    ray get_ray(float u, float v){return ray(origin, lower_left_corner + u*horizontal + v* vertical - origin);}

    vec3 lower_left_corner;
    vec3 horizontal;
    vec3 vertical;
    vec3 origin;
};

Now let’s expand the features of the camera model to include free positioning and depth of field(DOF). This time instead of fixed values, we are going to redefine the camera model with

1. camera world position lookfrom,
2. camera look-at position lookat
3. camera space up-vector vup
4. camera vertical field of view(FOV) vfov,
5. image plane width/height ratio aspect,
6. camera lense size aperture,
7. image plane to camera distance focus_dist.

By doing this we can still derive the final image plane size/position yet have better control on customizing camera parameters.

Camera Positioning

This section is corresponding to Chapter 10 “Positionable Camera” of Ray Tracing in One Weekend.

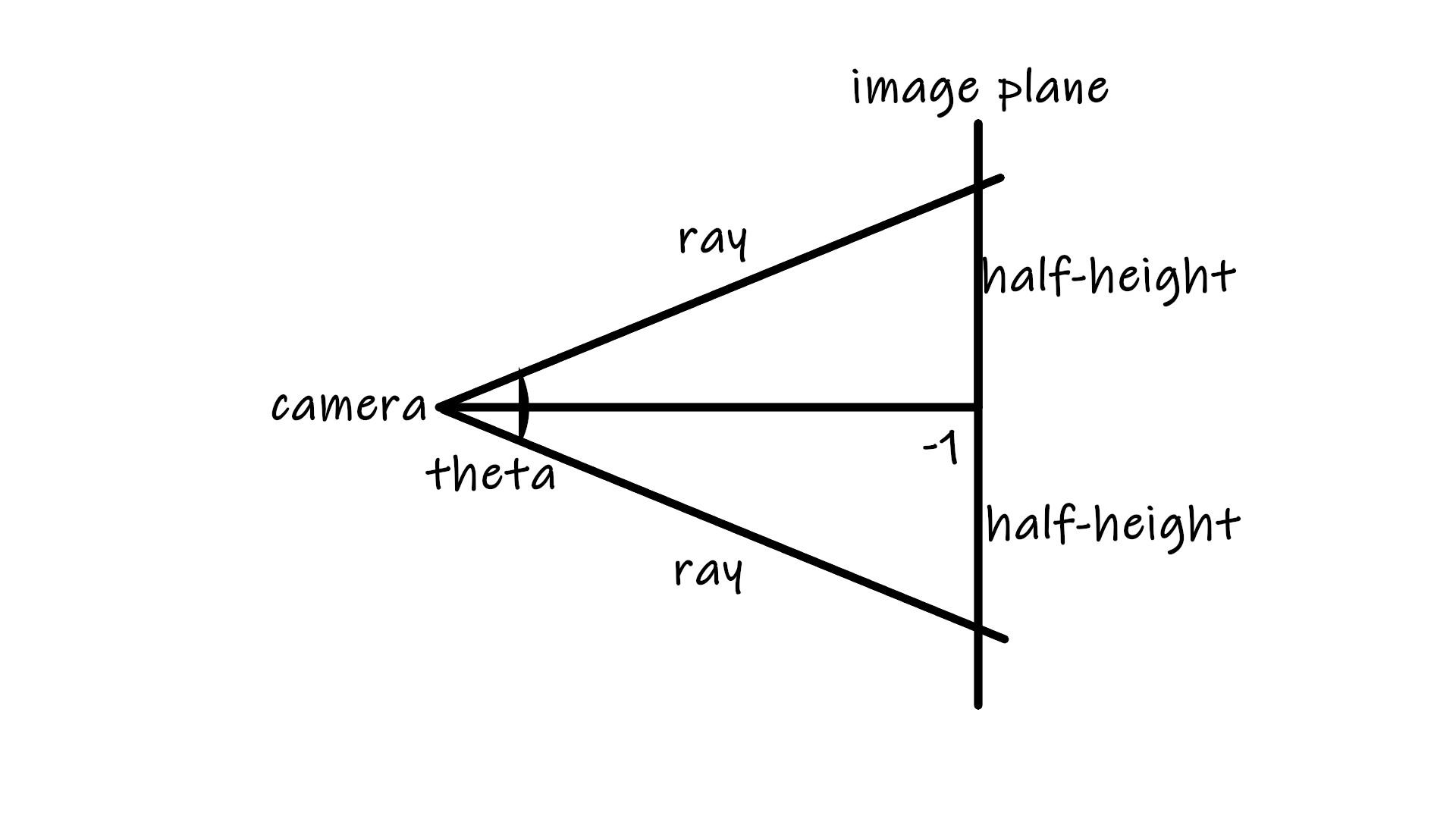
If the open angle of camera lense is theta, then half_height = tan(theta/2). theta is given by the vertical field of view(FOV) of the camera vfov, however in the unit of radian for convenience of calculation. So convertion theta = vfov*M_PI / 180 is needed where M_PI is value $\pi$ from <math.h> standard library.

Then if still keep the rest of camera settings the same, we can derive all the needed coordinates for image plane like this:

lower_left_corner(-half_width, -half_height,-1.0);
horizontal(2*half_width, 0.0, 0.0); // horizontal range
vertical(0.0, 2*half_height, 0.0);  // vertical range
origin = (0,0,0);

In world space, the set of vectors ${e1 = (1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1)}$ (the standard basis) forms an orthonormal basis. All vectors (x, y, z) in world space can be expressed as a sum of the basis vectors scaled ${\displaystyle (x,y,z)=xe_{1}+ye_{2}+ze_{3}}$.

Hence the previous derivation if put mathematically should be:

• lower_left_corner= origin - half_width * $e1$ - half_height * $e2$ - $e3$
• horizontal = 2 * half_width * $e1$
• vertical = 2 *half_height * $e2$

But if we want to transform camera to position lookfrom pointing to position lookat, we have to build a new orthonormal basis for camera space with the set of vetors $u,v,w$. They are defined as following:

w = unit_vector(lookfrom - lookat) // similar to the Z axis
u = unit_vector(cross(vup, w)) // similar to the X axis
v = cross(w, u) // similar to the Y axis

Conventionally, camera space up-vector vup is using (0，1，0).

Use the new basis $u,v,w$ to accordingly replace the old basis $e1,e2,e3$, we get the expanded camera model with new functionality of free positioning:

#include <math.h> // M_PI
#include "ray.h"
class camera {
public:
    camera(vec3 lookfrom, vec3 lookat, vec3 vup, float vfov, float aspect) {
        vec3 u, v, w;

        float theta = vfov*M_PI/180;
        float half_height = tan(theta/2);
        float half_width = aspect * half_height;
        origin = lookfrom;

        w = unit_vector(lookfrom - lookat);
        u = unit_vector(cross(vup, w));
        v = cross(w, u);

        lower_left_corner = origin - half_width*u - half_height*v -w;
        horizontal = 2*half_width*u;
        vertical = 2*half_height*v;
    }
    ray get_ray(float s, float t) {return ray(origin, lower_left_corner + s*horizontal + t*vertical - origin);}

    vec3 lower_left_corner;
    vec3 horizontal;
    vec3 vertical;
    vec3 origin;
};

Camera Depth of Field

This section is corresponding to Chapter 11 “Defocus Blur” of Ray Tracing in One Weekend.

Image from - Wikipedia

In optics, an aperture is a hole or an opening through which light travels. More specifically, the aperture and focal length of an optical system determine the cone angle of a bundle of rays that come to a focus in the image plane.

Image from - Wikipedia

Before, the focus length (or focus distance focus_dist) was defaulted at -1 on Z/w axises with image plane located at (0,0,-1). Now we are going to apply the customizable value focus_dist, and the coordinates for defining the image plane become:

lower_left_corner = origin - half_width*focus_dist*u - half_height*focus_dist*v - focus_dist*w;
horizontal = 2 * half_width*focus_dist*u;
vertical = 2 * half_height*focus_dist*v;

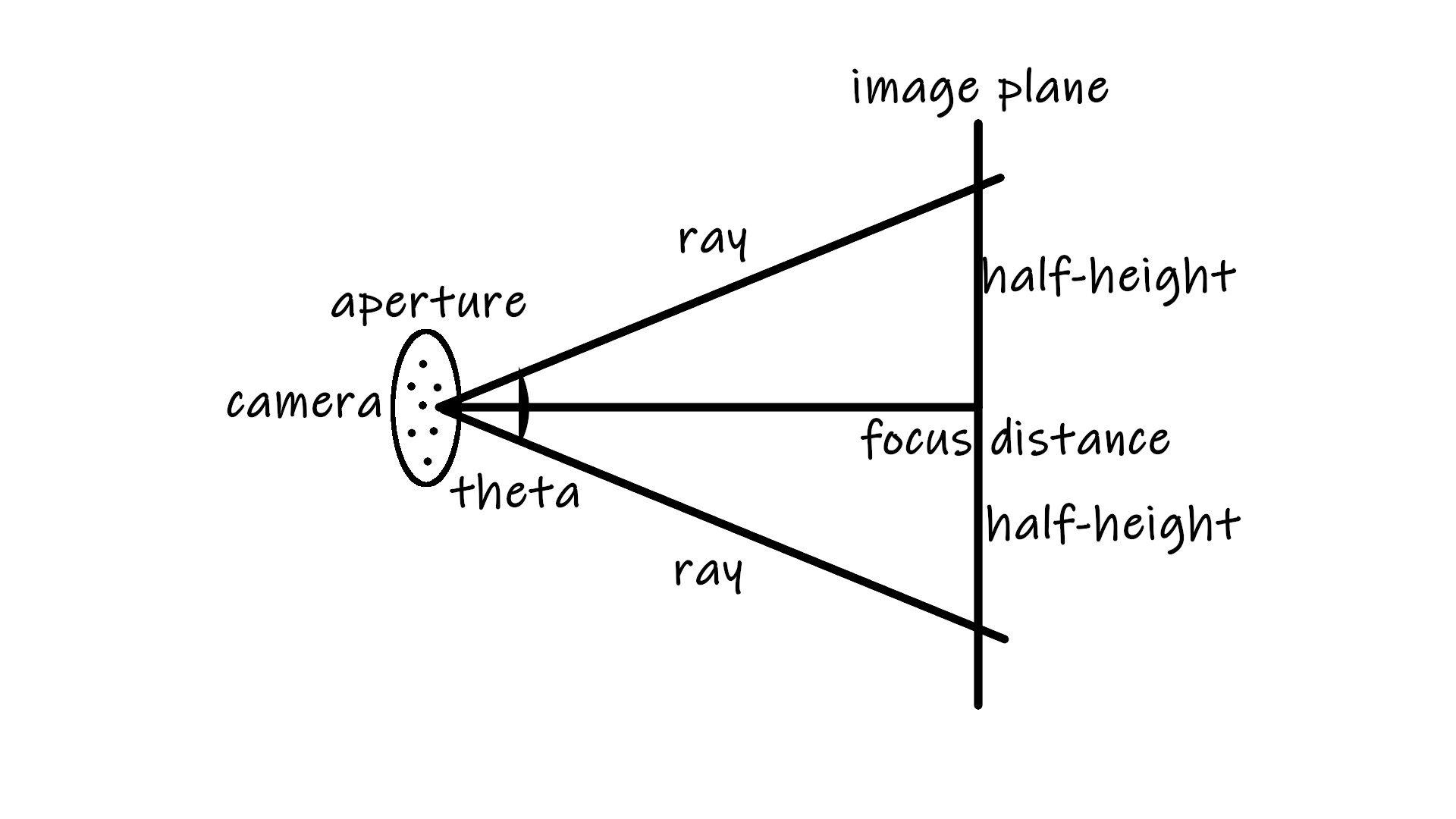
For the implementation of aperture, simply add a random value onto ray origin. The intensity of the randomness is controlled by lense radius lens_radius which is half of aperture value. So the implementation of the final camera model is:

#include "camera.h"
vec3 random_in_unit_disk() {...}

ray camera::get_ray(float s, float t) {
    vec3 rd = lens_radius * random_in_unit_disk(); // get random value
    vec3 offset = u * rd.x() + v * rd.y(); // calculate random offset vector
    // randomize ray casting
    return ray(origin + offset, lower_left_corner + s*horizontal + t*vertical - origin - offset);
}

And the corresponding final camera model full defination is:

class camera {
public:
    camera(vec3 lookfrom, vec3 lookat, vec3 vup, float vfov, float aspect, float aperture, float focus_dist)
    {
        lens_radius = aperture / 2;

        float theta = vfov * M_PI / 180;
        float half_height = tan(theta / 2);
        float half_width = aspect * half_height;
        origin = lookfrom;

        w = unit_vector(lookfrom - lookat);
        u = unit_vector(cross(vup, w));
        v = cross(w, u);

        lower_left_corner = origin - half_width*focus_dist*u - half_height*focus_dist*v - focus_dist*w;
        horizontal = 2 * half_width * focus_dist * u;
        vertical = 2 * half_height * focus_dist * v;
    }

    ray get_ray(float s, float t);

    vec3 origin;
    vec3 lower_left_corner;
    vec3 horizontal;
    vec3 vertical;
    vec3 u, v, w;
    float lens_radius;
};

TBC