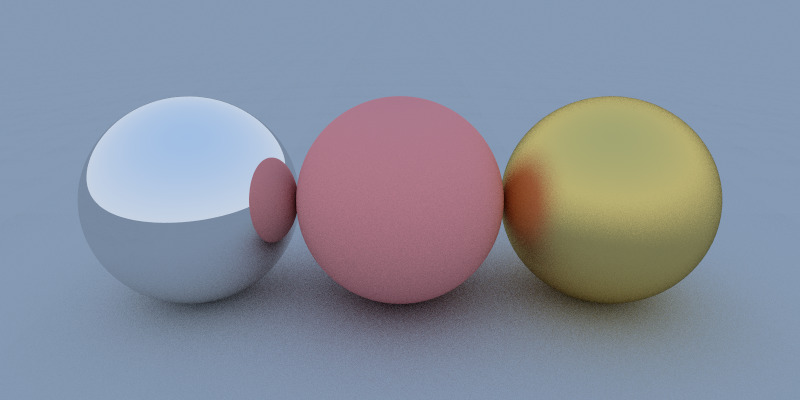Chapter 8 study note. Breakdown topics about Material base class, types of reflection, vector maths for calculating mirror reflection ray and blurry reflection implementation.

Material Base Class

Objects with different materials scatter the lights in different ways. It tells how rays interact with the surface.

When abstracting materials as a class, it should include functionalities like:

• taking the incoming ray ray& r_in and output reflected ray ray& scattered;
• calculating how much the ray should be attenuated - vec3& attenuation;
• gathering the info related to hit point and save into a hit_record struct rec.

And for struct hit_record, it packs up info like:

• parameter t of the ray that locates the intersection point;
• position of intersection point p;
• surface normal of intersection point normal;
• and also includes a reference to the material of the hit surface.

So we create an abstract class material with a definition of a pure virtual function scatter() that take care of all the functionalities mentioned above. Note that an abstract class constructs no objects but works as a template for its children.

#include "hitable.h"

/*
struct hit_record{
    float t;
    vec3 p;
    vec3 normal;
    material *mat_ptr;
};
*/

class material {
public:
    virtual bool scatter(
        const ray& r_in,
        const hit_record& rec,
        vec3& attenuation,
        ray& scattered) const = 0;
};

Here we create lambertian (diffuse material) and metal (reflecting material) material classes that inherited from material class. The children of an abstract class have to implement the pure virtual function.

Lambertian Material

Lambertian Material is an alternative technical name of diffuse material. Here we refractor the code about diffuse material from previous post.

Lambertian reflectance is the property that defines an ideal “matte” or diffusely reflecting surface. The apparent brightness of a Lambertian surface to an observer is the same regardless of the observer’s angle of view. More technically, the surface’s luminance is isotropic, and the luminous intensity obeys Lambert’s cosine law.

#include "material.h"

vec3 random_in_unit_sphere() {
    vec3 p;
    do{
        float random = drand48();
        p = 2.0 * vec3(random, random, random) - vec3(1,1,1);
    } while (p.squared_length() >= 1.0);
    return p;
}

class lambertian : public material {
public:
    lambertian(const vec3& a) : albedo(a) {}

    virtual bool scatter(
        const ray& r_in,
        const hit_record& rec,
        vec3& attenuation,
        ray& scattered) const {

        vec3 target = rec.p + rec.normal + random_in_unit_sphere();
        scattered = ray(rec.p, target - rec.p);
        attenuation = albedo;
        return true;
    }

    vec3 albedo;
};

Reflecting Materials

• Polished - A polished reflection is an undisturbed reflection, like a mirror or chrome.
• Blurry - A blurry reflection means that tiny random bumps on the surface of the material cause the reflection to be blurry.
• Metallic - A reflection is metallic if the highlights and reflections retain the color of the reflective object.
• Glossy - This term can be misused. Sometimes, it is a setting which is the opposite of blurry (e.g. when “glossiness” has a low value, the reflection is blurry). However, some people use the term “glossy reflection” as a synonym for “blurred reflection”. Glossy used in this context means that the reflection is actually blurred. (More later.)

Polished Reflecting Material

Reflection Vector

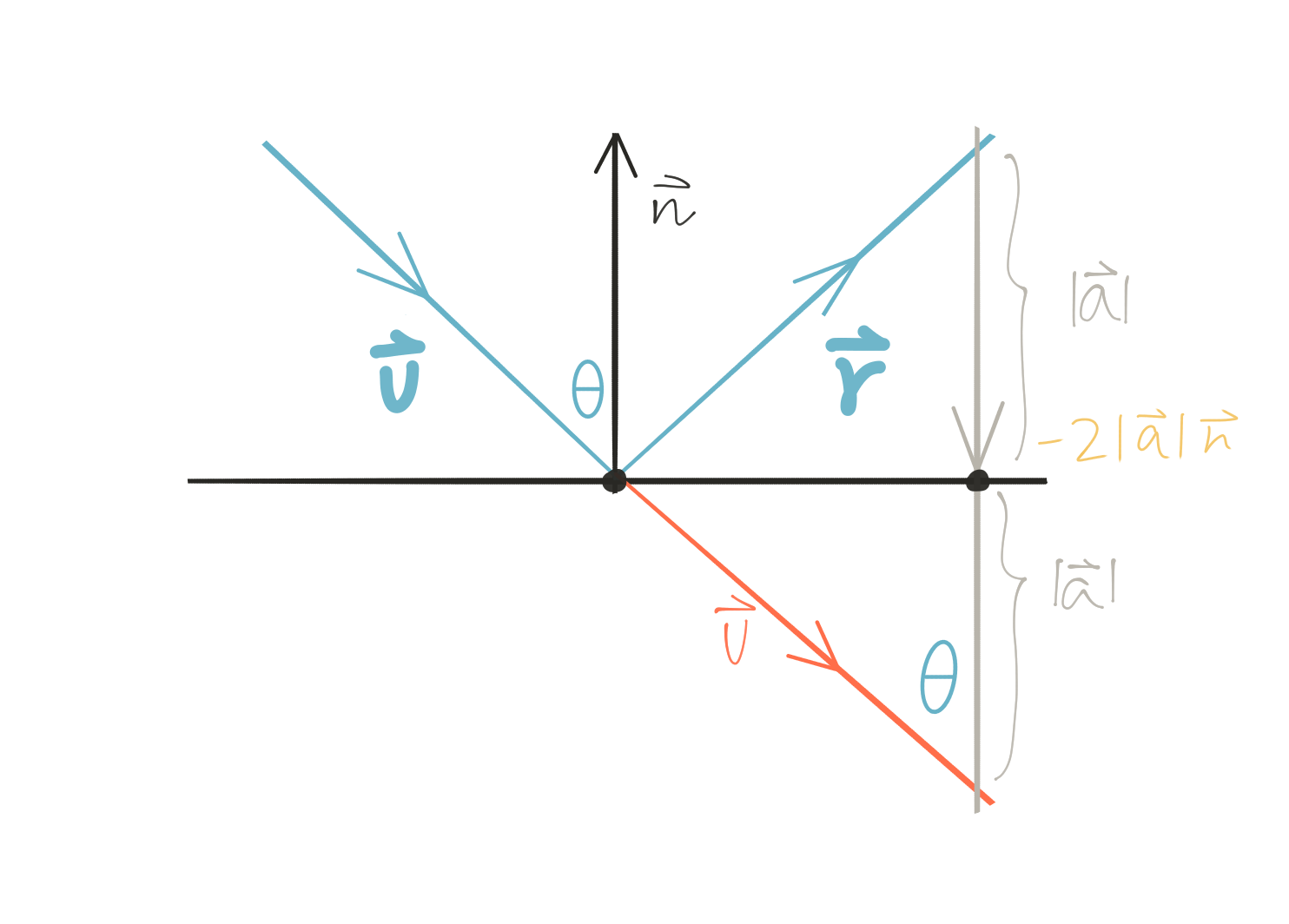
From the figure above, we get

\[\vec r = \vec v - (-2 * \vert \vec a\vert * \vec n)\]

where $\vert \vec a\vert = \vert \vec v\vert * cos(\theta)$.

Since $dot(\vec v, \vec n) = \vert \vec v\vert \vert \vec n\vert cos(\pi - \theta) = -\vert \vec v\vert cos(\theta)$, so $\vert \vec a\vert = -dot(\vec v, \vec n)$, and

\[\vec r = \vec v - (2 * dot(\vec v, \vec n) * \vec n)\]

vec3 reflect(const vec3& v, const vec3& n) {
    return v - 2 * dot(v,n) * n;
}

Note that here I’m deriving the calculation of the reflection vector according to the code from the book. Conventionally the direction of the incident vector is defined pointing toward the light source!

And the rest of code for metal material subclass is

#include "material.h"

class metal : public material {
public:
    metal(const vec3& a, float f) : albedo(a) {}

    virtual bool scatter(
        const ray& r_in,
        const hit_record& rec,
        vec3& attenuation,
        ray& scattered) const {

        vec3 reflected = reflect(unit_vector(r_in.direction()), rec.normal);
        scattered = ray(rec.p, reflected);
        attenuation = albedo;
        return (dot(scattered.direction(), rec.normal) > 0);
    }

    vec3 albedo;
};

Blurry Reflecting Material

To render a blurry reflecting look, we just need to add a little random vector random_in_unit_sphere() when calculating the directions of the reflected rays. Here we scale the random vector with a (0,1) float fuzz.

#include "lambertian.h" // random_in_unit_sphere()

// new constructor
metal(const vec3& a, float f) : albedo(a) {
    if (f<1) fuzz = f;
    else fuzz = 1;
}

    virtual bool scatter(
        const ray& r_in,
        const hit_record& rec,
        vec3& attenuation,
        ray& scattered) const {

        vec3 reflected = reflect(unit_vector(r_in.direction()), rec.normal);
        scattered = ray(rec.p, reflected + fuzz * random_in_unit_sphere()); // random
        attenuation = albedo;
        return (dot(scattered.direction(), rec.normal) > 0);
    }

    vec3 albedo;
    float fuzz; // random intensity
};