Study of raytracing has been progressing into the second book Ray Tracing: the Next Week, which is a little bit more advanced. This post is going to focus on some notes about Perlin Noise implementation.
Book Implementation Debug
50 shades of perlin noise... pic.twitter.com/IIWrVVsPAV
— ビクター (@viclw17) December 21, 2018
Follow the book I finally got the code working and render the correct images as shown above. One of the most annoying bugs I encountered was at some point the code failed to produce a valid .ppm image that can be opened by XnViewer (more details about image output see previous post: Raytracing - Image Output). I opened the image with text editor and notice there are lots of RGB values with all 3 elements as -2147483648. This made me wonder if the output of the noise function produced negative values that leads to the negative color value bug. I modified the noise_texture.h to output the noise value and that proved my speculation:
#ifndef NOISE_TEXTURE_H
#define NOISE_TEXTURE_H
#include "texture.h"
#include "perlin.h"
#include <iostream>
class noise_texture : public texture {
public:
noise_texture() {}
noise_texture(float sc) :scale(sc) {}
virtual vec3 value(float u, float v, const vec3& p) const {
float noise = perlin_noise.noise(scale*p); // bug!
std::cout << noise << std::endl;
return vec3(1.0,1.0,1.0) * noise;
}
perlin perlin_noise;
float scale;
};
#endif
Console output shows the range of noise output seems (-1,1):
Image outputing ...
-0.122155
-0.134105
-0.206453
-0.159719
-0.178172
0.112327
0.0720122
0.0839958
-0.157709
...
Solution is to scale and bias the noise to remap it from (-1,1) to (0,1):
// bug!
float noise = perlin_noise.noise(scale * p);
// fix: scale and bias!
float noise = 0.5 * (1 + perlin_noise.noise(scale * p));
Note: Negative/Invalid color value is one of the most common bugs of rendering… Always check the output range or make sure the output value not overflow the data type and cause strange value!
Building Up Perlin Noise
The implementation in the book is kinda overwhelming for me, so I decided to revisit later (after some emergency reading to refresh my C++ and basic math…)
As recommended by the book I digress a bit to read the post - Building Up Perlin Noise by Andrew Kensler. After a long-time debugging I finally get the code working.
Breakdown
Smoothstep
The original Perlin noise algorithm used a cubic Hermite spline of the form $s(t) = 3t^2 − 2t^3$. This particular function is also sometimes known as smoothstep.
In HLSL and GLSL, smoothstep implements the ${S} _{1}(x)$, the cubic Hermite interpolation after clamping:
\[{smoothstep} (x)=S_{1}(x)={\begin{cases}0&x\leq 0\\3x^{2}-2x^{3}&0\leq x\leq 1\\1&1\leq x\\\end{cases}}\]Again, assuming that the left edge is 0, the right edge is 1, with the transition between edges taking place where $0 ≤ x ≤ 1$.
float f( float t ) {
t = fabsf( t ); // float fabsf( float arg );
return t >= 1.0f ? 0.0f : 1.0f - ( 3.0f - 2.0f * t ) * t * t;
}
Surflet
Detailed explanation see post - Building Up Perlin Noise
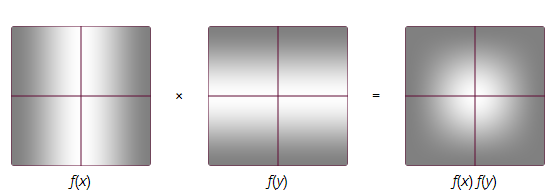
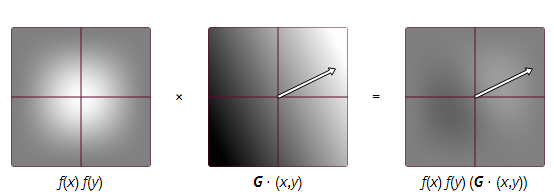
float surflet( float x, float y, float grad_x, float grad_y ) {
return f( x ) * f( y ) * ( grad_x * x + grad_y * y );
}
Initialization
static int const size = 256;
static int const mask = size - 1;
int perm[ size ];
float grads_x[ size ], grads_y[ size ];
// produce a random perm array and 2 arrays of random gradients
void init() {
for ( int index = 0; index < size; ++index ) {
int other = rand() % ( index + 1 );
if ( index > other )
perm[ index ] = perm[ other ];
perm[ other ] = index;
grads_x[ index ] = cosf( 2.0f * M_PI * index / size );
grads_y[ index ] = sinf( 2.0f * M_PI * index / size );
}
}
Evaluate Noise
float noise(float x, float y) {
float result = 0.0f;
int cell_x = floorf(x); // provide surflet grids
int cell_y = floorf(y); // provide surflet grids
for (int grid_y = cell_y; grid_y <= cell_y + 1; ++grid_y)
for (int grid_x = cell_x; grid_x <= cell_x + 1; ++grid_x) {
// random hash
int hash = perm[(perm[grid_x & mask] + grid_y) & mask];
// grads_x[hash], grads_y[hash] provide random vector
result += surflet(x - grid_x, y - grid_y, grads_x[hash], grads_y[hash]);
}
return result;
}
Full Implementation and Rendering
PGM Format
More about Netpbm format :
- Portable BitMap P1 .pbm 0–1 (white & black)
- Portable GrayMap P2 .pgm 0–255 (gray scale)
- Portable PixMap P3 .ppm 0–255 (RGB)
Here we are using Portable GrayMap.
#include <fstream>
using namespace std;
#define M_PI 3.1416
static int const size = 256;
static int const mask = size - 1;
int perm[ size ];
float grads_x[ size ], grads_y[ size ];
void init() {
// ...
}
float f(float t) {
// ...
}
float surflet(float x, float y, float grad_x, float grad_y) {
// ...
}
float noise(float x, float y) {
// ...
}
// rendering
int main() {
init();
const int dimension = 1000; // image is 1000x1000 pixels
// output into PGM image
ofstream outfile("render.pgm", ios_base::out);
outfile << "P2\n" << dimension << " " << dimension << "\n255\n";
int lattice = 20; // how many grid cells
int space = dimension / float(lattice);
for (int j = 0; j < dimension; j++) {
float y = (float)j / ((float)space); // cast to float!!!
for (int i = 0; i < dimension; i++) {
float x = (float)i / ((float)space);
float n;
// typical noise
n = noise(x, y); // (-1,1)
n = 0.5 * (n + 1.0); // bias and scale to remap from (-1,1) to (0,1)
// wooden-looking noise
//n = 20 * noise(x, y);
//n = n - floor(n);
// Map the values to the [0, 255] interval for color output
float color = floor(n * 255); // have to be int!
// or
// float color = int(n * 255); // this works the same as floor
outfile << color << " ";
}
outfile << "\n";
}
return 0;
}
Debug
First of all, remember to scale and bias the noise to remap it from [-1,1] to [0,1] to avoid negative color values!
Originally, I forgot to cast the loop indexes into float when dividing them by space. This cause the result always be truncated to 0 and produce an image of all black.
Also, at first I was so desperate to see the noise pattern so I just manually scale the noise: n = 128 + 128 * n; (which is fine) and output the values without casting them into integers outfile << n << " "; (WRONG!).
This somehow makes the PGM decoder confused with all those float values and produces a noisy image:

More resource
- Solarian Programmer ‘s post Perlin noise in C++11 helped me a lot on debugging and also offered a cool setup to generate wooden-looking noise pattern as noted in the code above.
- Also here is the clearest explanation I found so far:
END
